Wie finde ich die Höhe eines Trapezes?

Ein Trapez ist ein Viereck, zweidie Seiten davon sind parallel (dies sind die Basen des Trapezes, in den Figuren a und b angegeben) und die anderen zwei sind nicht (in der Figur, AD und CB). Die Höhe des Trapezes ist das senkrecht zu den Basen gezogene Segment h.
Wie finde ich die Höhe des Trapezes für bekannte Trapez- und Basislängen?

Um die Fläche S des Trapezes ABCD zu berechnen, verwenden wir die Formel:
S = ((a + b) × h) / 2.
Hier sind die Segmente a und b die Basen des Trapezes, h ist die Höhe des Trapezes.
Konvertieren Sie diese Formel, können wir schreiben:
h = 2 × S / (a + b)
Mit dieser Formel erhalten wir den Wert von h, wenn die Fläche S und die Längen der Basen a und b bekannt sind.
Beispiel:
Wenn bekannt ist, dass die Fläche des Trapezes S 50 cm² beträgt, beträgt die Länge der Basis a 4 cm, die Länge der Basis b 6 cm, und um die Höhe h zu finden, verwenden wir die Formel:
h = 2 × S / (a + b);
Wir ersetzen die bekannten Größen in die Formel.
h = (2 × 50) / (4 + 6) = 100/10 = 10 cm
Antwort: Die Höhe des Trapezes beträgt 10 cm.
Wie finde ich die Höhe eines Trapezes, wenn die Trapezfläche und die Länge der Mittellinie angegeben sind?

Wir verwenden die Formel zur Berechnung der Fläche des Trapezes:
S = m × h,
Hier ist m die mittlere Linie, h ist die Höhe des Trapezes.
Wenn die Frage auftaucht, wie man die Höhe des Trapezes findet, lautet die Formel:
h = S / m, wird die Antwort sein.
So können wir die Höhe des Trapezes h mit bekannten Werten der Fläche S und des Segments der Mittellinie m finden.
Beispiel:
Bekannte Länge der Mittellinie trapez m, die 20 cm sind, und die Fläche S, die auf 200 cm² entsprechen. Lassen Sie uns den Wert der Höhe des Trapezes h finden.
h = S / m.
Durch Einsetzen der Werte von S und m erhalten wir:
h = 200/20 = 10 cm
Antwort: Die Höhe des Trapezes beträgt 10 cm
Wie findet man die Höhe eines rechteckigen Trapezes?

Wenn das Trapez ein Viereck ist, mit zweiparallele Seiten (Basen) des Trapezes. Die Diagonale ist ein Segment, das zwei entgegengesetzte Ecken der Trapezwinkel verbindet (das Segment AC in der Figur). Wenn das Trapez rechteckig ist, wird anhand der Diagonalen die Höhe des Trapezes h gefunden.
Rechteckige Trapezes nannten diesen Trapezes, wobei eine der Seiten senkrecht zur Basis. In diesem Fall stimmt seine Länge (AD) mit der Höhe h überein.
Betrachten wir also das rechteckige Trapez ABCD,Wobei AD die Höhe ist, DC ist die Basis, AC ist die Diagonale. Wir verwenden den Satz des Pythagoras. Das Quadrat der Hypotenuse AC des rechtwinkligen Dreiecks ADC ist gleich der Summe der Quadrate seiner Schenkel AB und BC.
Dann können wir schreiben:
AC² = AD² + DC².
AD ist der Katheter des Dreiecks, die Seite des Trapezes und gleichzeitig seine Höhe. Schließlich ist das Segment von AD senkrecht zu den Basen. Seine Länge wird sein:
AD = √ (AC² - DC²)
Also, wir haben eine Formel für die Berechnung der Höhe des Trapezes h = AD
Beispiel:
Wenn die Länge der Basis des rechteckigen Trapezes (DC) 14 cm beträgt und die Diagonale (AC) 15 cm beträgt, verwenden wir das Pythagoras-Theorem, um die Höhe (AD-Seite) zu erhalten.
Sei x dann ein unbekanntes Bein eines rechtwinkligen Dreiecks (AD)
AC² = AD² + DC² kann aufgezeichnet werden
15² = 14² + ²²,
= = √ (15²-14²) = √ (225-196) = √29 cm
Antwort: Die Höhe des rechteckigen Trapezes (AB) beträgt √29 cm, was ungefähr 5.385 cm entspricht
Wie finde ich die Höhe eines gleichschenkligen Trapezes?

Ein gleichschenkliges Trapez wird als Trapez bezeichnet, yDie Längen der Seitenflächen sind gleich. Eine gerade Linie, die durch die Mitte der Basen eines solchen Trapezes gezogen wird, ist die Symmetrieachse. Ein besonderer Fall ist das Trapez, dessen Diagonalen senkrecht zueinander stehen, dann ist die Höhe h gleich der halben Summe der Basen.
Betrachten wir den Fall, wenn die Diagonalen nicht sindsind senkrecht zueinander. Im gleichseitigen (gleichschenkligen) Trapez sind die Winkel an den Basen und die Längen der Diagonalen gleich. Es ist auch bekannt, dass alle Ecken eines gleichseitigen Trapezes eine um dieses Trapez gezogene Kreislinie berühren.
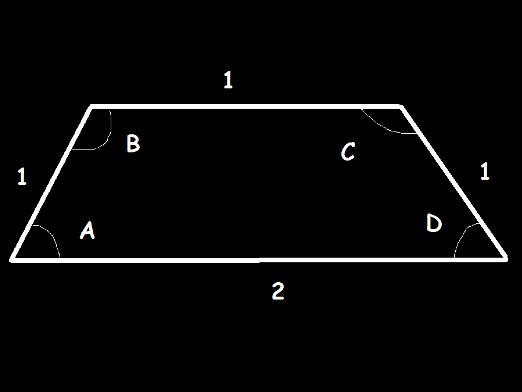
Betrachten Sie die Zeichnung. ABCD- gleichschenkliges Trapez. Es ist, dass Basis der parallelen Mittel Trapezes bekannt, BC = b parallel AD = a, Seite AB = CD = c, dann sind die Ecken an den Basen jeweils kann, Winkel geschrieben werden BAQ = CDS = α und der Winkel ABC = BCD = β. Daraus schließen wir, über die Gleichheit des Dreiecks ABQ Dreieck von SCD, dann schneiden
AQ = SD = (AD-BC) / 2 = (a-b) / 2.
Aufgrund der Problematik der Werte der Basen a und b und der Länge der lateralen Seite c finden wir die Trapezhöhe h gleich dem Segment BQ.
Betrachten Sie das rechtwinklige Dreieck ABQ. BO ist die Höhe des Trapezes senkrecht zur Basis AD und damit zum Segment AQ. Die Seite AQ des Dreiecks ABQ finden wir mit der von uns früher abgeleiteten Formel:
AQ = (a - b) / 2.
Wenn wir die Werte der beiden Schenkel eines rechtwinkligen Dreiecks haben, finden wir die Hypotenuse BQ = h. Wir verwenden den Satz des Pythagoras.
AB² = AQ² + BQ²
Wir ersetzen die Aufgabendaten:
c² = AQ² + h².
Wir erhalten eine Formel, um die Höhe eines gleichschenkligen Trapezes zu finden:
h = √ (c²-AQ²).
Beispiel:
Bei einem gleichschenkligen Trapez ABCD, wo die BasisAD = a = 10 cm, die Basis BC = b = 4 cm und die Seite AB = c = 12 cm. Betrachten wir unter solchen Bedingungen zum Beispiel, wie man das Trapez in der Höhe findet, ein gleichschenkliges Trapez eines ABCD.
Wir finden die Seite AQ des Dreiecks ABQ, indem wir die bekannten Daten ersetzen:
AQ = (a-b) / 2 = (10-4) / 2 = 3 cm.
Jetzt ersetzen Sie die Werte der Seiten des Dreiecks in der Formel des Pythagoras Theorems.
h = √ (c²-AQ²) = √ (12² - 3 ²) = √ 135 = 11,6 cm.
Antwort. Die Höhe h des gleichschenkligen Trapezes ABCD beträgt 11,6 cm.