Wie man einen Vektor baut?

Ein Vektor wird normalerweise ein Segment genannt, das hatangegebene Richtung. Sowohl der Anfang als auch das Ende des Vektors haben eine feste Position, mit deren Hilfe die Richtung des Vektors bestimmt wird. Betrachten wir genauer, wie man einen Vektor mit gegebenen Koordinaten konstruiert.

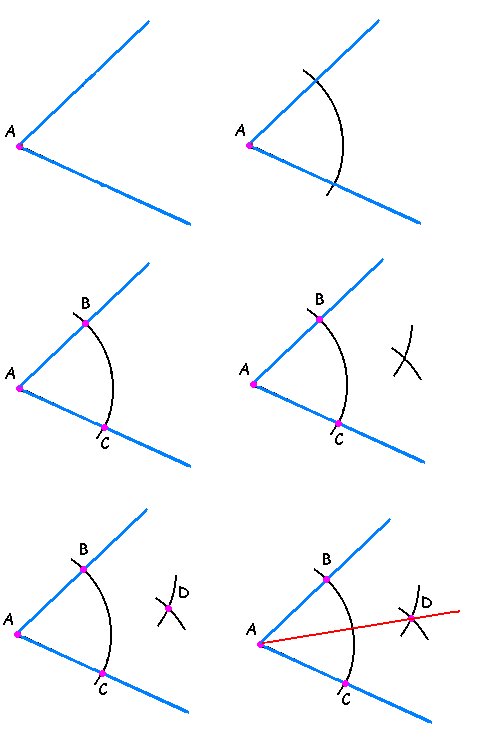
1. Zeichnen Sie ein Koordinatensystem (x, y, z) im Raum, markieren Sie einzelne Segmente auf den Achsen.
2. Legen Sie auf den beiden Achsen die erforderlichen Koordinaten fest und zeichnen Sie von ihnen die gepunkteten Linien parallel zu den Achsen zum Schnittpunkt. Lernen Sie den Schnittpunkt, den Sie brauchen, um die gepunktete Linie mit dem Ursprung zu verbinden.
3. Zeichnen Sie einen Vektor vom Ursprung zum resultierenden Punkt.
4. Stellen Sie auf der dritten Achse die gewünschte Zahl ein, zeichnen Sie durch diesen Punkt eine gepunktete Linie, die parallel zum konstruierten Vektor ist.
5. Zeichnen Sie am Ende des Vektors eine Strichpunktlinie parallel zur dritten Achse, bis sie die Linie vom vorherigen Punkt schneidet.
6. Verbinden Sie schließlich den Ursprung und den resultierenden Punkt.

Manchmal ist es erforderlich, einen Vektor zu konstruieren, der das Ergebnis der Addition oder Subtraktion anderer Vektoren sein wird. Deshalb betrachten wir nun Operationen mit Vektoren, wir lernen, wie man sie addiert und subtrahiert.

Operationen an einem Vektor

Geometrische Vektoren können hinzugefügt werdenauf verschiedene Arten. So ist zum Beispiel die gängigste Methode zum Hinzufügen von Vektoren die Dreiecksregel. Um zwei Vektoren gemäß dieser Regel hinzuzufügen, ist es notwendig, die Vektoren parallel zueinander so anzuordnen, dass der Anfang des ersten Vektors mit dem Ende des zweiten Vektors übereinstimmt und die dritte Seite des resultierenden Dreiecks der Summenvektor ist.

Sie können auch die Summe der Vektoren nach der Regel berechnenParallelogramm. Vektoren sollten von einem Punkt aus parallel zu jedem Vektor beginnen. Sie müssen eine Linie zeichnen, damit das resultierende Parallelogramm erhalten wird. Die Diagonale des konstruierten Parallelogramms wird die Summe dieser Vektoren sein.

Um zwei Vektoren zu subtrahieren, müssen wir die erste hinzufügenVektor und Vektor, der das Gegenteil von dem zweiten sein wird. Dazu wird auch die Regel des Dreiecks verwendet, die folgende Formel hat: Die Differenz von Vektoren, die so übertragen werden, dass ihre Anfänge übereinstimmen, ist ein Vektor, dessen Anfang mit dem Ende des Subtrahend-Vektors und auch mit dem Ende des dekrementierten Vektors übereinstimmt.