Wie finde ich den Sinus eines Winkels?
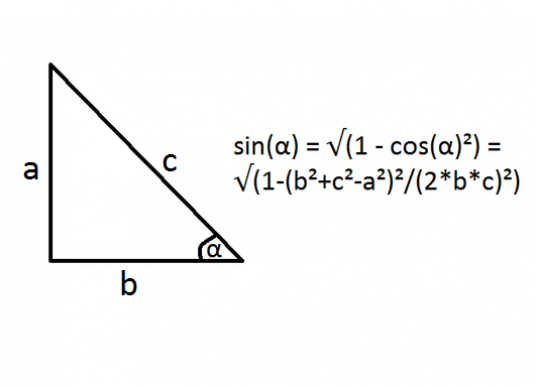
Sinus (sin) ist eine der direkten trigonometrischen Funktionen. Mehr Details dazu finden Sie in unserem Artikel Was ist ein Sinus?
Sinus eines Winkels in einem rechtwinkligen Dreieck
Bevor Sie herausfinden, wie Sie den Sinus eines Winkels finden, müssen Sie die Konventionen definieren. Angenommen, in einem rechtwinkligen Dreieck:
- α ist ein spitzer Winkel, dessen Sinus gefunden werden muss;
- с - Hypotenuse;
- b - zusammenhängender Kathete;
- a ist das entgegengesetzte Bein.
Dann um den Sinus des spitzen Winkels zu findenRechteck, ist es ausreichend, das Verhältnis der Länge des gegenüberliegenden Beines zu der Länge der Hypotenuse zu berechnen: sin (α) = a / c. Es ist daran zu erinnern, dass Sünde 90 ° immer 1 ist.
Sinus eines Winkels in einem beliebigen Dreieck
Finde den Sinus eines Winkels in einem beliebigen Dreieckam einfachsten mit dem Kosinussatz (cos): das Quadrat der Länge jeder Seite ist gleich der Summe der Quadrate der Längen der anderen beiden Seiten minus ihres Doppelproduktes durch den Kosinus des Winkels zwischen ihnen.
a² = b² + c² - 2 · b · c · cos (α)
Aus dieser Formel können Sie den Kosinus finden: cos (α) = (b² + c² - a²) / (2 * b * c)
Und da für denselben Winkel sin (α) ² + cos (α) ² = 1 und dies eine Konstante ist, können wir eine Formel zur Bestimmung des Sinus ableiten:
sin (α) = √ (1 - cos (α) ²) = √ (1- (b² + c²-a²) ² / (2 * b * c) ²).
Ausführlich wird das Finden des Sinus eines Winkels unter Verwendung des Kosinus in unserem Artikel beschrieben, wie man einen Sinus findet, wenn der Kosinus bekannt ist.