Wie löst man magische Quadrate?

Ein magisches Quadrat wird normalerweise ein Puzzle genanntwie ein Sudoku. Dies ist ein Quadrat, dessen Zellen mit Zahlen gefüllt sind, so dass die Summe am Ende jeder Zeile, Spalte und Diagonale gleich ist. In den magischen Puzzlequadraten werden einige Zahlen weggelassen, und sie müssen so angeordnet werden, dass sie den oben beschriebenen Zustand der gleichen Summe beobachten. Wie löst man magische Quadrate?

Wege, magische Quadrate zu lösen

Um die Lösung der magischen Quadrate zu seinWahr, du musst die magische Menge kennen, die du erhalten solltest, wenn du Zahlen in Zeilen, Spalten und Diagonalen hinzufügst. Danach ist es viel einfacher, die fehlenden Nummern anzuordnen. Wie finden Sie diesen Betrag?

Methode 1

Die einfachste Version des magischen Quadrats -Wenn eine der Zeilen, eine der Spalten oder eine der Diagonalen vollständig mit Zahlen gefüllt ist. In diesem Fall bleibt es nur, um die Summe dieser Zahlen zu berechnen und die Lösungen zu wählen.

Methode 2

Die Summe der Zahlen an den Enden von Zeilen, Spalten undDiagonalen können mit speziellen Formeln berechnet werden. In diesem Fall unterscheidet sich die Formel für Quadrate mit einer geraden Anzahl von Zellen in einer Zeile von Quadraten mit einer ungeraden Anzahl von Zellen.

Also, für gerade Quadrate ist die Formel geeignet:

• n + ((n + 1) * n * (n - 1) / 2), wobei n die Anzahl der Zellen in einer Zeile ist.

Für ungerade Quadrate gilt die folgende Formel:

• n * (n² +1) / 2, wobei n auch die Anzahl der Zellen in einer Zeile ist.

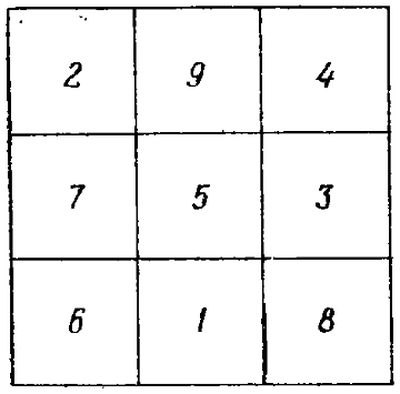
Beispiellösung

Betrachte die Lösungen des magischen Quadrats von NeunZellen mit Zahlen von 1 bis 9. Zuerst berechnen wir die Menge, die an den Enden erhalten werden sollte. In einer Zeile haben wir 3 Zellen, also n = 3. Ersetzen Sie den Wert in der Formel:

• 3 * (3² +1) / 2 = 3 * 10/2 = 15

Jetzt wählen wir Zahlen, so dass die Summe gleich 15 ist.

Außerdem wird der Algorithmus ein wenig benötigenräumliche Vorstellung. Setze Nummer 1 in die Mitte der oberen Zeile. Jede nächste Zahl setzen wir schräg nach oben. Versuchen Sie, 2 zu setzen. Aber es gibt keine Zellen, wenn wir ein anderes des gleichen imaginären über unser Quadrat ersetzen, erscheint die Zahl 2 in der unteren rechten Ecke davon

neues Quadrat. Wir übertragen es auf unseren Platz und legen ihn in die untere rechte Ecke. Die Zahl 3 ist auch diagonal nach rechts oben platziert - und wieder gibt es keine Zelle, mit Hilfe eines imaginären Quadrats wissen wir, dass sich ihr Platz in der Mitte der linken Spalte befindet. Auf die gleiche Weise wird die Zahl 4 gesetzt, aber diese Zelle wird von einer Einheit besetzt - in diesem Fall stellen wir sie direkt unter die Zahl 3. Die Zahl 5 auf der Diagonalen oben und rechts von 4 ist in der Mitte und die Zahl 6 in der oberen rechten Ecke. Nummer 7 mit der Phantasie sollte in der unteren linken Ecke sein. Aber da ist schon 4, also legen wir es direkt unter die Zahl 6. Die Zahl 8 entpuppt sich als ein imaginäres Quadrat in der linken oberen Ecke und die Zahl 9 in der verbleibenden Zelle in der Mitte der rechten Spalte. Der allgemeine Algorithmus ist wie folgt: setze die nächste Zahl rechts oben entlang der Diagonale, wenn es keinen Platz gibt - wende ein imaginäres Quadrat an, und wenn die Zelle besetzt ist, dann lege die Zahl direkt unter die vorherige.

Lesen Sie auch Wie funktioniert das magische Quadrat?