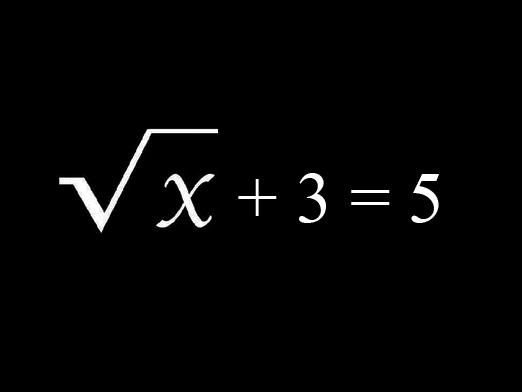Wie finde ich die Wurzel der Gleichung?

Einer der Hauptabschnitte der Mathematik ist ein Abschnitt zum Lösen von Gleichungen und zum Finden der Wurzel von Gleichungen.
Bevor Sie die Wurzel der Gleichung finden, müssen Sie zuerst herausfinden, was es ist.
Die Wurzel der Gleichung ist der Wert des UnbekanntenWerte in der Gleichung mit lateinischen Buchstaben (häufiger - x, y, aber es kann andere Buchstaben geben). Dies wurde in unserem Artikel erwähnt - Was ist die Wurzel der Gleichung.
Überlegen Sie, wie Sie alle Wurzeln, verschiedene Arten von Gleichungen und spezifische Beispiele finden.
Die Gleichung der Form ax + b = 0
Dies ist eine lineare Gleichung mit einer Variablen, wobei a und b Zahlen sind und x die Wurzel der Gleichung ist.
Die Anzahl der Wurzeln der Gleichung hängt von den Werten von a und b ab:
- Wenn a = b = 0, dann hat die Gleichung eine unendliche Anzahl von Wurzeln.
- Wenn a = 0 ist, ist b nicht 0, dann hat die Gleichung keine Wurzeln.
- Wenn a nicht gleich 0 ist, dann finden wir die Wurzel durch die Formel: x = - (b / a)
Beispiel:
- 5x + 2 = 0
- a = 5, b = 2
- x = - (2/5)
- x = -0,4
Antwort: Die Wurzel der Gleichung ist 0.4
Die Gleichung ist ax2 + bx + c = 0.
Dies ist eine quadratische Gleichung. Es gibt mehrere Möglichkeiten, die Wurzeln in der quadratischen Gleichung zu finden. Wir betrachten eine allgemeine Lösung, die sich für alle Werte von a, b und c eignet.
Zuerst müssen wir die Diskriminante (D) dieser Gleichung finden.
Dafür gibt es die Formel:
- D = b2-4ac
Je nachdem, was der Diskriminant gelernt hat, gibt es 3 Optionen für weitere Lösungen:
- Wenn D> 0, dann die Wurzeln von 2. Und sie werden nach den Formeln berechnet:
- x1= (-b + √ D) / 2a.
- x2= (-b - √ D) / 2a
- Wenn D = 0, dann ist die Wurzel eins - es kann durch die Formel gefunden werden: x = - (b / 2a)
- Wenn D <0, dann hat die Gleichung keine Wurzeln.
Beispiel:
- x2+ 3x-4 = 0
Hier gilt a = 1, b = 3, c = -4
- D = 32 - (4 * 1 * (- 4))
- D = 9- (-16)
- D = 9 + 16
- D = 25
D> 0, dann gibt es 2 Wurzeln in der Gleichung.
- √ D = √ 25 = 5
Wir ersetzen alle Werte in unserer Formel:
- x1 = (-3 + 5) / 2 * 1
- x1= 2/2
- x1= 1
- x2= (-3-5) / 2 * 1
- x2= (-8) / 2
- x2= -4
Antwort: Die Wurzeln der Gleichung sind 1 und -4.
Die Gleichung der Form ax3+ bx2+ cx + d = 0
Dies ist eine kubische Gleichung.
Es gibt spezielle Formeln des Cardano-Mathematikers, von denen man eine solche Gleichung lösen kann, aber sie sind sehr komplex. Wir werden den anderen, verständlicheren Weg gehen.
Kubische Gleichungen haben immer mindestens einsroot, und sein Wert ist normalerweise eine ganze Zahl von -3 bis 3. Das heißt, wir werden in der verfügbaren Gleichung für x Zahlen ersetzen: -3, -2, -1, 0, 1, 2 und 3. Dies wird X sein1.
Es ist viel einfacher und schneller als es scheint und sicherlich einfacher als die Verwendung der Cardano-Formeln.
Nachdem wir x gefunden haben1 , gehe zur Suche X2 und X3.
Zu diesem Zweck teilen wir unsere Gleichung in (x-x1) - dies kann durch die Klammern gemacht werden. Wir müssen eine quadratische Gleichung haben, die wir in diesem Artikel ein wenig höher gelöst haben.
Beispiel:
- x3 - 3x2 - 13x + 15 = 0
Durch die Auswahlmethode finden wir heraus, dass X1= 1, das heißt, wir müssen unsere Gleichung in (x-1) teilen
Als Ergebnis erhalten wir:
- x2 - 2x - 15 = 0
Wir haben eine quadratische Gleichung erhalten. Wir lösen es wie oben. Und wir kommen zu der Tatsache, dass es 2 Wurzeln hat: - 3 und 5.
Antwort:
- Die Wurzeln der Gleichung: x1= 1, x2= -3, x3 = 5.
Weitere Informationen finden Sie im Artikel So lösen Sie die Wurzeln.